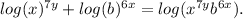Question

Write the expression as a single logarithm 7log(x) y + 6 log(b) x

Answer 1

Answer:
`log(x)^(7y)+log(b)^(6x)=log(x^(7y)b^(6x)).`

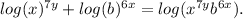
Explanation:

Given logarithm expression

`7log(x)^y + 6 log(b)^x.`

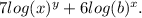
We need to write it as a single logarithm expression.

First we need to apply exponent rule of logs to remove 7 and 6 in front of logs.

`n log(p) = log(p)^n`

`7log(x)^y + 6 log(b)^x.= log(x)^(7y)+log(b)^(6x)`.

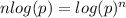
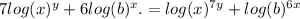Now, we need to apply product rule of logs
`log(p)+log(q) = log(pq)`.

`log(x)^(7y)+log(b)^(6x)=log(x^(7y)b^(6x)).`

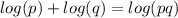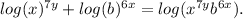
Therefore, final answer is
`log(x)^(7y)+log(b)^(6x)=log(x^(7y)b^(6x)).`