Question

two cars are traveling on two different roads that are perpendicular to each other. on a coordinate map, the first started from the point (-3,2) and stopped at (1,-2). the second car started from (-1,-2) and stopped at (3,y). what is the y-coordinate of the final destination of the second car?

Answer 1

Since the roads are perpendicular to each other. And for perpendicular lines, product of slopes is equal to -1 .

So for the first car , with the points , (-3,2),(1,-2), slope is

`m_(1) = (-2-2)/(1-(-3)) = (-4)/(4) = -1`

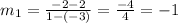
And for the second car, with points (-1,-2),(3,y), slope is

`m_(2) = (y-(-2))/(3-(-1)) = (y+2)/(4)`

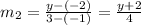
And product of slopes have to be -1, that is

`m_(1)*m_(2) =-1`

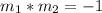
Substituting the values of the two slopes

`=> -1* (y+2)/(4) =-1 \\ =>(y+2)/(4) =1`

Multiplying both sides by 4

`y+2 =4 \\ y=4-2 \\ y=2`

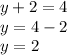
And that's the missing value of y coordinate .