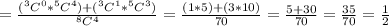a. The probability of picking exactly two $10 bills is

b. The probability of picking at most one $5 bill is

Step-by-step explanation
Number of $10 bills
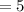
and number of $5 bills
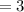
Total number of bills= 5+3 = 8. You need to randomly pick 4 bills, so the total possible outcome

a.
For getting exactly two $10 bills, you need to pick two $10 bills and two $5 bills. That means we will pick two $10 bill from 5 bills and two $5 bills from 3 bills.
So, the probability
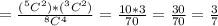
b.
For getting at most one $5 bill, you need to pick either zero or one $5 bill.
If you pick zero $5 bill, that means there are four $10 bills
and if you pick one $5 bill, that means there are three $10 bills.
So, the probability