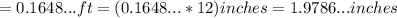The width of the border will be 0.1648... ft or 1.9786... inches.
Step-by-step explanation
Lets assume, the width of the border is
 ft.
ft.
The rectangular garden is 15 ft in length and 7 ft in width. So, the area of the garden
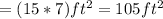
Now, the length of the garden including border
 and the width of the garden including border
and the width of the garden including border
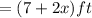
So, the area of the garden including the border
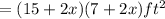
Thus the area of the border
![=[(15+2x)(7+2x)-105] ft^2](https://img.qammunity.org/2019/formulas/mathematics/high-school/wtc0i79kyqtjy3wkdjyvq2ftu2kk4pn5n4.png)
Total amount of premixed cement needed is 1 yard³ = 27 ft³
As the depth of the border is 44 inches or
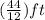 or
or
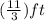 , so....
, so....
![(11)/(3)[(15+2x)(7+2x)-105] = 27\\ \\ 11(105+44x+4x^2 -105)=81\\ \\ 11(4x^2+44x)=81\\ \\ 44x^2+484x-81=0](https://img.qammunity.org/2019/formulas/mathematics/high-school/2tfrj0ftswq01mybdvqvpr2ws1zw0icpqo.png)
Using quadratic formula....

(Negative value ignored)
So, the width of the border