Answer:
Domain:
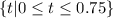 ,
,
Range:

Explanation:
We have been given that a bicyclist travels at a constant speed of 12 miles per hour for a total of 45 minutes. We are asked to write the domain and range of the function in set notation.

Since the bicycle travels at constant rate, so the distance traveled by bicycle at any time t (in minutes) would be
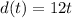 .
.
We know that domain of a function is set of all values of independent variable. We can see that independent variable is time (t).
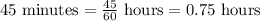
Since the bicycle travels for a total of 45 minutes that is 0.75 hours , so domain of our function is restricted to interval
 that is
that is
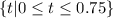 in set notation.
in set notation.
To find the upper limit of range of our given function, we will substitute
 in our function as:
in our function as:
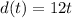
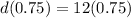
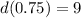
Therefore, the range of our given function would be
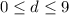 that is
that is
 in set notation.
in set notation.