Answer: The number of onion cells that are needed to line up end to end are 40,000
Step-by-step explanation:
We are given:
Length of microscopic slide = 8 cm
Length of 1 onion cell =
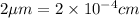 (Conversion factor:
(Conversion factor:
 )
)
To calculate the number of onion cells required, we divide the length of microscopic slide to the length of 1 onion cell, we get:
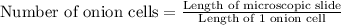
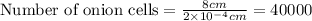
Hence, the number of onion cells that are needed to line up end to end are 40,000