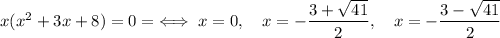First of all, move all terms to the same side:
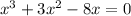
You can factor an x, which means that
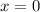 is a solution:
is a solution:
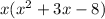
This expression is further factorizable if the quadratic equation has any solution. Using the quadratic formula, we can find that they are

So, we have