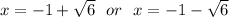x^2 + 2x - 5 = 0
Keep the x^2-term and the x-term on the left side. Add 5 to both sides to get rid of the -5 from the left side.
x^2 + 2x = 5
The term you need to add to the left side to complete the square is the square of half of the coefficient of the x-term. The x-term is 2x. The coefficient of the x-term is 2. Half of 2 is 1. 1 squared is 1. That means you need to add 1 to the left side to complete the square. The rule with equations is that you need to add the same thing to both sides of the equation, so we must add 1 to both sides.
x^2 + 2x + 1 = 5 + 1
x^2 + 2x + 1 = 6
Now the left side is a perfect square. You can express it as the square of a binomial.
(x + 1)^2 = 6
There is a rule: if w^2 = k, k being a non-negative number, then w = sqrt(k) or w = -sqrt(k). We now apply his rule. In our case, our w is x + 1.
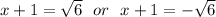
Now we solve each equation above by subtracting 1 from both sides.