Question

Quadrilateral STWR is inscribed inside a circle as shown below. Write a proof showing that angles T and R are supplementary.

Answer 1

Observe the given figure.

Here, angle T and R are the inscribed angles.

And sum of inscribed angles is half of measure of intercepted arcs.

Since, the measure of intercepted arcs is 360 degrees.

Therefore,
`\angle T + \angle R = (1)/(2) * 360 ^(\circ)`

`\angle T + \angle R = 180 ^(\circ)`

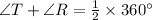
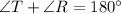
Hence, the sum of the two angles is 180 degrees.

Therefore, these are the supplementary angles.

Therefore, angle T and angle R are supplementary angles.

Hence, proved.