Question

How can you write the expression with rationalized denominator 2+sqrt 5/2-sqrt 5

Answer 1

`(2+\sqrt5)/(2-\sqrt5)=((2+\sqrt5)^2)/(4-5)=(4+4\sqrt5+5)/(-1)=-(9+4\sqrt5)=-9-4\sqrt5`

Answer 2

Option D -
`-9-4\sqrt5`

Explanation:

Given : Expression
`(2+\sqrt5)/(2-\sqrt5)`

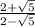
To write : The expression with rationalized denominator.

Solution :

Step 1 - Write the expression

`=(2+\sqrt5)/(2-\sqrt5)`

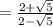
Step 2- Rationalized denominator i.e, multiply and divide the expression with
`2+\sqrt5`

`=(2+\sqrt5)/(2-\sqrt5)* (2+\sqrt5)/(2+\sqrt5)`

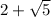
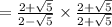
Step 3 - Using identity
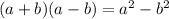`(a+b)(a-b)=a^2-b^2` in the denominator.

`=((2+\sqrt5)^2)/(2^2-(\sqrt5)^2)`

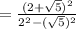
Step 4 - Solve the expression

`=(2^2+(\sqrt5)^2+2(2)(\sqrt5))/(4-5)`

`=(4+5+4\sqrt5)/(-1)`

`=-9-4\sqrt5`

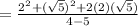
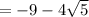
The solution is rewrite as
`(2+\sqrt5)/(2-\sqrt5)=-9-4\sqrt5`

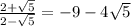
Therefore, Option D is correct.