![[\text{A}^(-)] / [\text{HA}] \approx 0.525](https://img.qammunity.org/2019/formulas/chemistry/college/hwth8bi0a270r85ird62jkkioft04l6kwm.png)
Step-by-step explanation:
The Henderson-Hasselbalch equation estimates the value of
![[\text{A}^(-)] / [\text{HA}]](https://img.qammunity.org/2019/formulas/chemistry/college/4goq2jm1fcjm19md4yjn1kflenjt4uqf5q.png) of a buffer given its
of a buffer given its
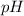 and the acid dissociation constant of weak acid
and the acid dissociation constant of weak acid
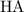 :
:
![pH \approx pK_(a) + \text{log}_(10) ([\text{A}^(-)] / [\text{HA}])](https://img.qammunity.org/2019/formulas/chemistry/college/k2cr2uup7obaqu21ko6yjnz5nvm54rsrqj.png)
Rearranging:
![[\text{A}^(-)] / [\text{HA}] \approx 10^(-pH) / 10^(-pK_a)](https://img.qammunity.org/2019/formulas/chemistry/college/dhnex2jj66bvrzlpvowcgflj8lb3myq9j4.png)
The question states that
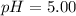 and
and
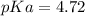
Thus
![[\text{A}^(-)] / [\text{HA}] \approx 10^(-5.00) / 10^(-4.72) = 0.525](https://img.qammunity.org/2019/formulas/chemistry/college/m32ilayxcx1e4kk88550w0r01mnakl763w.png)
Reference:
Gurinder Khaira and Alexander Kot (UCD), "Henderson-Hasselbalch Approximation," Chemistry Libretext