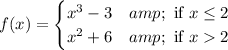Question

Which of the following functions is graphed below??

Answer 1

It should be B on my opinion
I hope this help you

Answer 2

The required piece-wise function is

`f(x)=\begin{cases}x^3-3 & \text{ if } x\leq 2 \\ x^2+6 & \text{ if } x>2 \end{cases}`

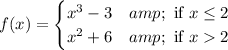
Explanation:

From the given graph it is clear that it is a piece-wise function because it is braked in two parts.

One part is defined for x≤2 and other part is defined for x>2 because left curve has closed circle at x=2 and right curve has open circle at x=2.

The y-intercept of the function is -3. From the given graph it is clear that the graph defined for x≤2 is a graph of cubic function that shifts 3 units down. So, the required function for x≤2.

`f(x)=x^3-3`

From the given graph it is clear that the right curve passes through the point (3,15) and moves towards (2,10).

The function
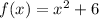`f(x)=x^2+6` satisfied by both the points. So, the required function for x>2.

`f(x)=x^2+6`

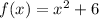
Therefore the required piece-wise function is

`f(x)=\begin{cases}x^3-3 & \text{ if } x\leq 2 \\ x^2+6 & \text{ if } x>2 \end{cases}`