Question

Pierre deposits $9,000 in a certificate of deposit that pays 1.4% interest, compounded semi-annually

How much interest does the account earn in the first six months?
What is the balance after six months?

Answer 1

Interest = $63

Balance = $2,063

Explanation:

Compound Interest Formula

`\boxed{\sf I=P\left(1+(r)/(n)\right)^(nt) -P}`

where:

• I = Total interest.
• P = Principal amount.
• r = Interest rate (in decimal form).
• n = Number of times interest is applied per year.
• t = Number of time periods (years) elapsed.

Given:

• P = $9,000
• r = 1.4% = 0.014
• n = 2 (semi-annually)
• t = 0.5 (half a year)

Substitute the given values into the formula and solve for I:

`\implies \sf I=9000\left(1+(0.014)/(2)\right)^(2 * 0.5)-9000`

`\implies \sf I=9000\left(1+0.007\right)^(1)-9000`

`\implies \sf I=9000\left(1.007\right)-9000`

`\implies \sf I=9063-9000`

`\implies \sf I=63`

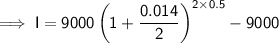
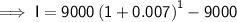
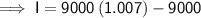
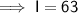
Therefore, the account earns $63 interest in the first six months.

The balance after six months is $2,063.