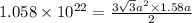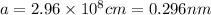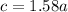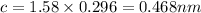Question

Titanium (ti) has an hcp crystal structure, a density of 4.51 g/cm3, and the atomic weight for ti, ati= 47.9 g/mol.(a)what is the volume of its unit cell in cubic meters?(b)if the c/a ratio is 1.58, compute the values of cand

a.

Answer 1

(a)
`V_C=1.058x10^(-28)(m^3)/(UnitCell)`

(b)
`a=2.96x10^(-10)m\\c=4.67x10^(-10)m`

Step-by-step explanation:

Hello,

(a) In this case, we apply the following formula in order to solve for the volume per unit cell,
`V_C`:

`\rho =(a*M)/(V_C*N_A)`

Now, a accounts for the atoms into the HCP which are 6, M accounts for the atomic mass of titanium and
`N_A` for the Avogadro number, thus:

`V_C=(a*M)/(\rho *N_A)=(6*47.9g/mol)/(4.51g/cm^3*6.022x10^(23)UnitCell/mol)=1.058x10^(-22)(cm^3)/(UnitCell)*(1m^3)/(100^3cm^3)=1.058x10^(-28)(m^3)/(UnitCell)`

(b) Here, for the HCP:

`V_C=6cR^2√(3)`

We know that
`R=a/2` and
`c/a=1.58`, thus:

`V_C=6c(a/2)^2√(3)\\V_C=6a*1.58(a/2)^2√(3)\\V_C=16.4a^3/4\\a=\sqrt[3]{(4*1.058x10^(-28)(m^3)/(UnitCell))/(16.4) } \\a=2.96x10^(-10)m\\c=1.58a\\c=1.58*2.96x10^(-10)m\\c=4.67x10^(-10)m`

Best regards.

Answer 2

(a)

The volume of unit cell is given by:

`\rho = (nA)/(V_cN_A)`

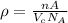
where
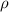`\rho` is density, n is the number of atoms in the given HCP crystal, A is the atomic weight of titanium,
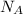`N_A` is the Avogadro's number.

Putting the values in the formula:

`4.51 = (6* 47.9)/(V_C* 6.022* 10^(23))`

`V_C = 1.058 * 10^(-22) cm^(3)/unit cell`

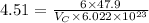
Thus, the volume of unit cell is
`V_C = 1.058 * 10^(-28) m^(3)/unit cell`

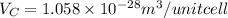
(b)

The edge length of HCP is given by:

`V_C = 6R^(2)c√(3)`

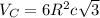
where R is the atomic radius of the atom and c is the height of hexagon.

Substituting
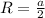`R = (a)/(2)` in the above equation of
`V_C`:

`V_C = 6((a)/(2))^(2)c√(3)` =
`(3√(3)a^(2)c)/(2)`

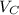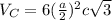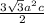
Substituting the values:

`1.058* 10^(22) = (3√(3)a^(2)* 1.58a)/(2)`

`a = 2.96 * 10^(8) cm = 0.296 nm`

`c = 1.58 a`

`c = 1.58* 0.296 = 0.468 nm`