Question

I cannot solve this. can u plis solve this huhuhuhuhuhuhuhuhuhu

Answer 1

Not middle school.

`f(x) = \frac 1 8 ( e^(4x) + 3 )`

We're after the integral from 0 to B, less the right triangle OAB. So we need to find A and B.

`A = f(0) = \frac 1 8(1 + 3) = \frac 1 2`

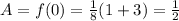
The slope at 0 is
`f'(0)`

`f'(x) = \frac 1 8 ( 4 e^(4x) ) = \frac 1 2 e^(4x)`

`f'(0) = \frac 1 8(4) = \frac 1 2`

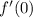
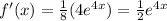
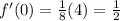
The normal has negative reciprocal slope, so m=-2 through (0,1/2)

`y - \frac 1 2 = -2 x`

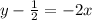
The x intercept (when y=0) is B:

`-\frac 1 2 = -2B`

`B = \frac 1 4`

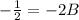
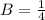
The right triangle area is

`\frac 1 2 AB = (1)/(16)`

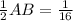
The integral is

`\displaystyle \int_0^(\frac 1 4) \frac 1 8 ( e^(4x) + 3 ) dx = \frac 1 8 ( \frac 1 4 e^(4x) + 3x ) |_0^(\frac 1 4)`

`= \frac 1 8( (e/4 + 3/4) - 1/4) = (1)/(32)(e+2)`

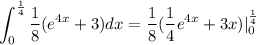
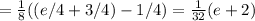
The area we seek is the difference,

`A= (1)/(32)(e+2) - \frac {1}{16} = (e)/(32)`

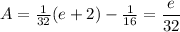
Answer: e/32