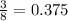Solution: We are given that a fair coin is tossed three times. The sample space associated with the three tosses of fair coin is:
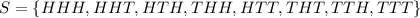
We have to find the probability of getting exactly one tail.
From the above sample space, we clearly see there are three outcomes which favors the probability of exactly one tail.
n( 1 tail) =

Therefore the probability of exactly one tail is