Solution: We are given that a basket contains three green apples and six red apples.
Three apples are randomly selected from the basket.
Now the probability of selecting first apple green is
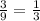
The probability of selecting second apple green is
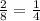
The probability of selecting third apple green is

Therefore, the probability of selecting three green apples is:
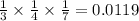 or 1.19%
or 1.19%
Now how many red apples must be added to the basket in order to make the above probability smaller than 0.1%
If we add 11 red apples to the basket, then there will be 17 red apples and 3 green apples in the basket. Therefore, the probability of selecting three green apples if three apples are randomly selected is:
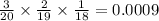 or 0.09%
or 0.09%
Therefore, we need to add 11 red apples to the basket to make this probability smaller than 0.1%