![[\text{C}_4 \text{H}_6] \approx 5.2 * 10^(-3) \; \text{mol} \cdot \text{L}^(-1)](https://img.qammunity.org/2019/formulas/chemistry/college/u02ua3qvu73966a50qey6urvnsr0t821pk.png)
Step-by-step explanation:
From the rate law:
![\text{d} [\text{C}_4 \text{H}_6] /\text{d}t = - 0.014 \cdot [\text{C}_4 \text{H}_6]^(2)](https://img.qammunity.org/2019/formulas/chemistry/college/8qsbvp0h3f3kyup073l86c192uv1n4a39a.png)
where
![[\text{C}_4 \text{H}_6]](https://img.qammunity.org/2019/formulas/chemistry/college/hhlz5wopvc2h1i4iz3s8w4fj86n0r7lr6d.png) the reactant concentration, in
the reactant concentration, in
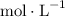 (or equivalently,
(or equivalently,
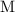
 the time into the reaction process, in seconds, and
the time into the reaction process, in seconds, and
![\text{d} [\text{C}_4 \text{H}_6] /\text{d}t](https://img.qammunity.org/2019/formulas/chemistry/college/1a6r6fls3vpen2qrfi9amh4bgfh64bbu36.png) the reaction rate in differential form.
the reaction rate in differential form.
Note the negative sign in front of the right hand side of the equation. Rearrange the rate law expression to separate the two variables,
- concentration
![[\text{C}_4 \text{H}_6]](https://img.qammunity.org/2019/formulas/chemistry/college/hhlz5wopvc2h1i4iz3s8w4fj86n0r7lr6d.png) and
and - time
 .
.
![-[\text{C}_4 \text{H}_6]^(-2) \cdot \text{d} [\text{C}_4 \text{H}_6] = 0.014 \cdot \text{d}t](https://img.qammunity.org/2019/formulas/chemistry/college/b0wk5kczt9o5yqz2rli3egghlvyd60jj8u.png)
Implicitly integrate both sides of the expression (with the power rule) to obtain the general expression (i.e., the one with the arbitary constant "
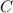 ") for concentration
") for concentration
![[\text{C}_4 \text{H}_6]](https://img.qammunity.org/2019/formulas/chemistry/college/hhlz5wopvc2h1i4iz3s8w4fj86n0r7lr6d.png) at given time
at given time
 :
:
![\int(- [\text{C}_4 \text{H}_6]^(-2) )\cdot \text{d} [\text{C}_4 \text{H}_6] = \int 0.014 \cdot \text{d}t](https://img.qammunity.org/2019/formulas/chemistry/college/p8l9dfzadqd5htuq6biwrc6sopsvurelec.png)
![[\text{C}_4 \text{H}_6]^(-1) = 0.014 \cdot \text{t} + C](https://img.qammunity.org/2019/formulas/chemistry/college/p0iz53e6gqgdfaphqutjq37my7v6lq373p.png)
![[\text{C}_4 \text{H}_6] = 1/ (0.014 \cdot \text{t} + C)](https://img.qammunity.org/2019/formulas/chemistry/college/vjik3du7w1t5v52ai4r3aqir3iaj4or1d2.png)
Now, solve for the value of
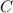 for this particular configuration (i.e., with an initial,
for this particular configuration (i.e., with an initial,
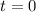 concentration
concentration
![[\text{C}_4 \text{H}_6] = 0.025 \text{mol}\cdot \text{L}^(-1)](https://img.qammunity.org/2019/formulas/chemistry/college/d51yj0l8ohqje50iwn0mmzgxnhnufjfqq5.png) , as seen in the question)
, as seen in the question)
![1/ (0.014 \cdot \text{t} + C) = 1\; /\; C = [\text{C}_4 \text{H}_6]_{\text{initial}} = 0.025](https://img.qammunity.org/2019/formulas/chemistry/college/khuqqwfvwloi8yni21lyxnari85tchm6gw.png)
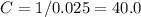
Thus, the
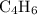 concentration at time
concentration at time
 given an initial
given an initial
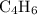 concentration of
concentration of
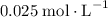 would be
would be
 = 1/(0.014 \cdot t +40)](https://img.qammunity.org/2019/formulas/chemistry/college/fa8js490gja1h50xpi6wcucok9260tpbxz.png)
where again,
 the time into the reaction in seconds.
the time into the reaction in seconds.
The question is asking for the concentration at

 = 5.2 * 10^(-3) \; \text{mol} \cdot \text{L}^(-1)](https://img.qammunity.org/2019/formulas/chemistry/college/8x3arlt0eov2zcqcmxeyiaorpphl2pfqla.png)
Reference:
Lannah Lua, Ciara Murphy, and Victoria Blanchard, "Second-Order Reactions," Libretext Chemistry