For this case, the first thing we must do is define variables.
We have then:d
x: cost of each small pizza
y: cost of each liter of soda
z: cost of each salad.
We write the equation that models the problem:


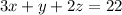
From equation 3 we clear y:
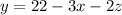
Substituting in equation 2 we have:
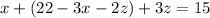
Rewriting:
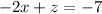
From here, we clear the value of z:
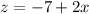
Then, we substitute the value of z and y in equation 1:
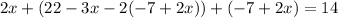
From here, we clear x:
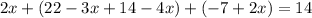
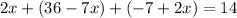
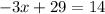

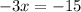
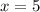
Then, the value of z is:
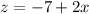
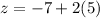
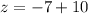
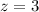
Finally, the value of y is:
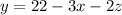


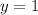
Answer:
$ 5: cost of each small pizza
1 $: cost of each liter of soda
3 $: cost of each salad.