We have been given that the garden and the walkway around its perimeter have an area of 378 square feet.
Let us suppose the width of the walkway is x feet. Please see the attached image.
From the attached image, the area of the garden and the walkway around its perimeter is given by
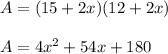
Now, the area is given bt 378 square feet. Hence, we have

Therefore, the width of walkway is 3 feet.