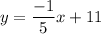Question

At the curb a ramp is 11 inches off the ground. the other end of the ram rests on the street 55 inches from the curb write a linear equation in slope intercept form that relates the height y of the ramp to he distance x from the curb

Answer 1

d slope is 0-11 / 55-0 = -11/55 = -1/5
intercept is (0,11)

y=-1/5x + 11

Answer 2

The linear equation in slope intercept form that relates the height y of the ramp to he distance x from the curb is:

`y=(-1)/(5)x+11`

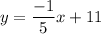
Explanation:

If we model this equation on a coordinate plane we see that the ramp passes through the point (0,11) and (55,0)

where the horizontal axis i.e. the x-axis represent the distance of the ramp from the curb and the vertical axis represent the height y of the ramp.

We know that the ramp satisfies a linear relationship.

Hence, the slope is constant between two points.

i.e. the slope of a line passing through (a,b) and (c,d) is calculated by:

`Slope=(d-b)/(c-a)`

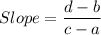
Also, the slope intercept of a line is given by:

y=mx+b

where m is the slope and b is the y-intercept.

From the given problem we have slope as:

`m=(0-11)/(55-0)\\\\\\m=(-11)/(55)\\\\\\m=-(1)/(5)`

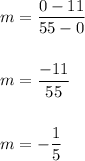
Also, y-intercept is: b=11

( Since the y-intercept is the value where x=0 )

The equation is given as:

`y=(-1)/(5)x+11`