Question

Evan has graphed the point (5, 7) and he wants to reflect it over the line y=-2/5x+6. He predicts that the reflected point will have coordinates (2, 2). Without graphing, can you confirm his answer or show that he cannot be correct?

Answer 1

Given that Evan has graphed the point (5, 7) and he wants to reflect it over the line y=-2/5x+6. He predicts that the reflected point will have coordinates (2, 2).

Now we have to check if his answer is correct or not without graphing. Yes this is possible without graphing.

If his answer is correct then the line passing through points (5,7) and (2,2) will be perpendicular to the given line.

slope of line passing through the points (5,7) and (2,2) is given by :

`m=(y_2-y_1)/(x_2-x_1)`

`m=(7-2)/(5-2)`

`m=(5)/(3)`

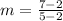
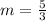
slope of the given line
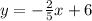`y=-(2)/(5)x+6` is
`-(2)/(5)`

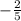
We know that If the two lines are perpendicular then product of their slopes equals -1

`-(2)/(5)*(5)/(3) = -(2)/(3)`

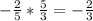
Which is not -1. That means both lines are not perpendicular.

Hence his answer is wrong.