Question

A store offers two payment plans. under the installment plan, you pay 25% down and 25% of the purchase price in each of the next 3 years. if you pay the entire bill immediately, you can take a discount of 6% from the purchase price. assume the product sells for $100. a-1. calculate the present value of the payments if you can borrow or lend funds at an interest rate of 4 percent. (do not round intermediate calculations. round your answer to 2 decimal places.) pv of installment plan $ 94.38 a-2 which is a better deal? installment plan pay in full b-1. calculate the present value if the payments on the 4-year installment plan do not start for a full year. (do not round intermediate calculations. round your answer to 2 decimal places.) pv of installment plan $ 69.38 b-2. which is a better deal? installment plan pay in full

Answer 1

a-1 . The Present Value of the installment plan is $94.38.

We calculate the PV of $25 for each of the three following years with the following formula:

`PV_(Annuity) = Constant Payment * PVIFA_(0.04,3)`

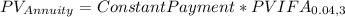
where

PVIFA = Present Value interest factor of an annuity of $1 at 4% for 3 years.

`PVIFA_(0.04,3) = 2.77509103`

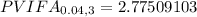
We can ascertain this in excel by using the syntax : =pv(0.04,3,-1).

In this syntax, 0.04 is the interest rate, 3 is number of periods and since the annuity is $1 we write 1. We need to put in -1 because otherwise, we'll get the answer as a negative number. This is because excel treats any Present Values as outflows, and records them as negative.

Substituting the values above in the preceding equation we get,

`PV_(Annuity) = 25 * 2.77509103`

`PV_(Annuity) = 69.3772758`

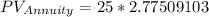
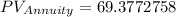
In order to find the Present Value of the installment plan, we need to add the down payment of $25. So,

`PV_(instalment) = $25 + 69.3772758`

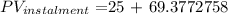
PV of instalment = $94.38

a-2. We get a 6% discount when we pay in full, so the purchase price of the product becomes:

`Purchase price = 100 - (100*0.06)`

`Purchase price = $94 (100 - 6)`

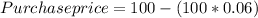
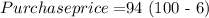
Since the purchase price of the pay in full plan is lesser than that of the installment plan, the pay in full plan is a better option.

b-1. The Present Value of the installment plan is $90.75.

Since the first instalment falls due only after one year, we calculate the PV of $25 each of four years with the following formula:

`PV_(Annuity) = Constant Payment * PVIFA_(0.04,4)`

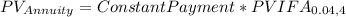
where

PVIFA = Present Value interest factor of an annuity of $1 at 4% for 4 years.

`PVIFA_(0.04,4) = 3.62989522`

We can ascertain this in excel by using the syntax : =pv(0.04,4,-1).

Substituting the values above in the preceding equation we get,

`PV_(Annuity) = 25 * 3.62989522`

`PV_(Annuity) = 90.7473806`

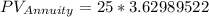
b-2. In this case, the PV of the pay in full plan remains at $94 while that of the instalment plan falls to $90.75. Since the PV of the Instalment plan is lower, we'll choose the instalment plan.