Question

Sara has six necklaces, but her mother will only allow her to wear two at a time. How many different combinations of two necklaces can Sara wear?

Answer 1

6C2 = (6 x5)/(2 x 1) = 15 difference combinations

Answer 2

15 different combinations

Explanation:

Sara has six necklaces, but her mother will allow her to wear two at a time.

So we calculate different combinations of two necklaces by this formula:

`(n!)/(r!(n-r)!)`

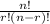
Where n = 6 and r = 2

Now put the values

`(6!)/(2!(6-2)!)`

`(6* 5* 4* 3* 2* 1)/(2!(6-2)!)`

`(720)/(2* 1(4)!)`

`(720)/(2* 1(4* 3* 2* 1))`

`(720)/(2(24))`

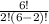
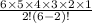
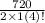
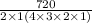
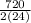
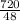`(720)/(48)` = 15 combinations

Sara can wear 15 different combinations of two necklaces.