Question

I need help with 15,18,19,23,and 24. Thanks.

Answer 1

For #15 & 18, the x-coordinate for the midpoint can be found by adding the x-values and dividing by 2. the y-coordinate of the midpoint can be found by add the y-values and dividing by 2.

I will do #15 as an example:

(3, -5) and (7, 9)

M = (
`(x1 + x2)/(2)`,
`(y1 + y2)/(2)`)

= (
`(3 + 7)/(2)`,
`(-5 + 9)/(2)`)

= (
`(10)/(2)`,
`(4)/(2)`)

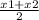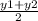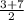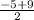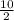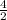= (5, 2)

#19) use the same concept as in #15, however you have the midpoint and one of the endpoints so split the x's and y's into two separate equations.

endpoint is (5, -6), midpoint is (4, 3)

xM =
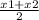`(x1 + x2)/(2)` yM =
`(y1 + y2)/(2)`

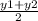
Multiply both sides of both equations by 2 to eliminate the denominator

2(xM) = x₁ + x₂ 2(yM) = y₁ + y₂

Now, plug in the midpoint and endpoint values and then solve.

2(4) = 5 + x₂ 2(3) = -6 + y₂

8 = 5 + x₂ 6 = -6 + y₂

3 = x₂ 12 = y₂

Endpoint coordinate is (3, 12)

For #23 & 24, use the distance formula: d =
`\sqrt{(x_(2) - x_(1))^(2) + (y_(2) - y_(1))^(2)}`

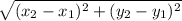
I will do #23 as an example: (13,2) and (7, 10)

d =
`\sqrt{(7 - 13)^(2) + (10 - 2)^(2)}`

=
`\sqrt{(-6)^(2) + (8)^(2)}`

=
`√(36 + 64)`

=
`√(100)`

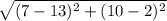
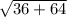
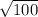
= 10