Question

Please help! Thanks in advance.

Find the values of a and b such that 1 and 4 are zeros of

`f(x) = 2x^4-5x^3-14x^2+ax+b`

Answer 1

In this problem, we need to plug in the given x values for
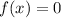
`f(x)=0` and find a and b.

When we plug in 1, we get:
`2 * {1}^(4) - 5 * {1}^(3) - 14 * {1}^(2) + a * 1 + b = 0`

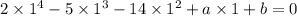
Simplify:

`2 - 5 - 14 + a + b = 0`

`- 17 + a + b = 0`

`a + b = 17`

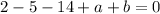
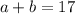
We got our first statement about the values of the variables. If we find one more we can find those 2 variables.

We have another given root: 4.

Plug it in:

`2 * {4}^(4) - 5 * {4}^(3) - 14 * {4}^(2) + a * 4 + b = 0`

`512 - 320 - 224 + 4a + b = 0`

`- 32 + 4a + b = 0`

`4a + b = 32`

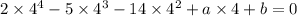
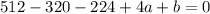
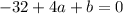
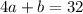
Now we have our second one. We can combine them:

`a + b = 17 \\ 4a + b = 32`

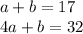
I use elimination method which is easier here.

Multiply the top equation by -1:
`- a - b = - 17 \\ 4a + b = 32`

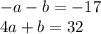
Add them up:

`3a = 15`

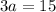
Simplify:

`a = 5`

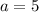
Now we have a, we can plug in one of those equations to find b:

`5 + b = 17`

`b = 17 - 5`

`b = 12`

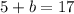
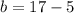
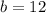
So, the answers are
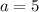
`a=5` and
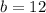
`b=12` .