Question

there was a total of 548 dollars collected for tickets to the school play.The adult tickets cost 6 dollars,and the student tickets cost 4 dollars.If 12 more student tickets were sold than adult tickets,find the numbers of adult and student tickets sold.

Answer 1

This is a systems of equations problem. To begin, we need to set up our equations.

If there was a total of 548 dollars collected, and adult tickets cost $6, and students tickets $4, this equation represents that situation.

6a + 4s = 548

The variable a stands for adult, and variable s for student. Now, if 12 more student tickets were sold than adults, this would represent that.

a + 12 = s

Now we can set it up as a systems of equations.

`\left \{ {{6a + 4s = 548} \atop {a + 12 = s}} \right.`

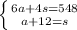
Because s = a + 12, we can plug that in into the other equation.

6a + 4(a + 12) = 548

Distribute 4.

6a + 4a + 48 = 548

Combine like terms.

10a + 48 = 548

Subtract 48 from both sides.

10a = 500

Divide both sides by 10.

a = 50

Plug a into the original equation.

50 + 12 = s

Combine like terms.

62 = s

There were 62 student tickets and 50 adult tickets sold.