Question

Given the arithmetic sequence: u(1)= 124, u(2)= 117, u(3)= 110, u(4)=103,...

u(k) is the first term in the sequence that is negative
find the value of k

Answer 1

We are given

arithmetic sequence: u(1)= 124, u(2)= 117, u(3)= 110, u(4)=103

so, first term is 124

u(1)= 124

now, we can find common difference

`d=u(2)-u(1)`

`d=117-124`

`d=-7`

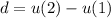
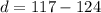
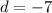
now, we can find kth term

`u(k)=u(1)+(k-1)d`

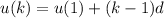
now, we can plug values

and we get

`u(k)=124+(k-1)*-7`

`u(k)=124-7k+7`

`u(k)=131-7k`

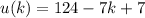
u(k) must be negative

so,

`u(k)=131-7k<0`

`131-7k<0`

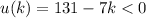
now, we can solve for k

`7k>131`

`k>18.714`

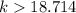
so, it's closest integer value is

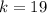`k=19`..............Answer