Answer:
15 is the answer.
Explanation:
Initial number of selling = 30 at the cost $2.50 each
on increasing $0.50 cost on each we have 2 fewer selling
that is number of selling be x so its 30-2x
cost of selling for 30-2x will be = 2.50+0.50x
revenue = (30-2x)(2.5+0.5)
the value of x for which revenue is increased
(30-2x)(2.5+0.5x)>0
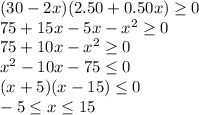
so the maximum value of x is 15