Question

The terminal side of θ passes through the point (10, 6). What is the exact value of cos θ in simplified form?

Answer 1

`(5√(34))/(34)`

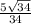
Explanation:

The formula for cos θ is a/r. A is the first number (10) and b is the second number (6). R is the hypoteneuse which can be found through r =
`\sqrt{a^(2) + b^(2) }`.

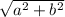In the equation you'd write that as r =
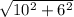`\sqrt{10^(2) + 6^(2)` which can be simplified to
`\sqrt{136`.

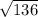You end up with
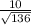`(10)/(√(136) )` and you simplify this by doing
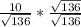`(10 )/(√(136) ) * (√(136) )/(√(136) )`, ending with the result of
`(5√(34))/(√(34) )`.

(I also got this answer right on the test.)