Question

IF A, B AND C ARE INTERIOR ANGLES OF Δ ABC,

SHOW THAT
SEC² (B+C / 2) -1 = COT²A/2

TRIGONOMETRY CLASS 10 MATHS.
PLS HELP ME ASAP.

Answer 1

First, it would be nice if we could put all of our angle measures in terms of a single variable. Since we're dealing with the interior angles of a triangle, and since the interior angles of a triangle add to 180°, we can say that

A + B + C = 180, or equivalently,

B + C = 180 - A

Knowing this, we can replace the B + C on the left side of the equation with 180 - A so that our equation reads:

`\sec^2\big({(180-A)/(2)\big)-1=\cot^2\big({(A)/(2) }\big)`

Doing a little tidying, we can rewrite the term
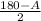`(180-A)/(2)` as

`(180-A)/(2) =(180)/(2)-(A)/(2) =90-(A)/(2)`

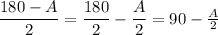
By definition,
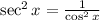`\sec^2x=(1)/(\cos^2x)`, so I'd like to rewrite the left side of the equation with these last two things in mind:

`\sec^2\big({(180-A)/(2)\big)-1=(1)/(\cos^2(90-(A)/(2))) -1`

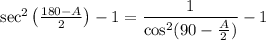
`cos((90-x))=sin(x)`, so we can rewrite the left side again as

`(1)/(\sin^2\big((A)/(2)\big)) -1`

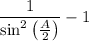
Next, we note that - by definition,
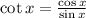`\cot{x}=(cos(x))/(sin(x))`. This allows us the rewrite the right side of the equation as

`\cot^2\big((A)/(2)\big)=\frac{\cos^2\big((A)/(2)\big)}{\sin^2\big({(A)/(2)}\big)}`

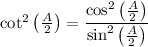
And our full equation as

`(1)/(\sin^2\big((A)/(2)\big)) -1 = \frac{\cos^2\big((A)/(2)\big)}{\sin^2\big({(A)/(2)}\big)}`

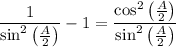
Next, we want to take advantage of the most essential trig identity,
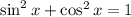`\sin^2{x}+\cos^2{x}=1`, specifically the form we get by subtracting
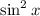`\sin^2x` from either side:
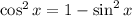`\cos^2{x}=1-\sin^2{x}`. We can transform the left side of this problem's equation into the same form by multiplying either side by
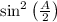`\sin^2\big((A)/(2)\big)`. Here's what we get out of that:

`\sin^2\big((A)/(2)\big)\Bigg((1)/(\sin^2\big((A)/(2)\big)) -1\Bigg) = \sin^2\big((A)/(2)\big)\Bigg( \frac{\cos^2\big((A)/(2)\big)}{\sin^2\big({(A)/(2)}\big)}\Bigg) \\\\\\ 1-\sin^2\big((A)/(2)\big)=\cos^2\big((A)/(2)\big)`

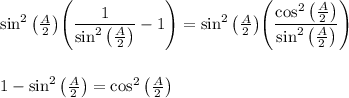
The identity
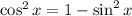`\cos^2x=1-\sin^2x` tells us this statement must be true, so we're done at this point.