Answer:
The range that 95% of the bags fall within is (4.02,5.98)
Explanation:
Given : A potato sorting machine produces 5 lb bags of potatoes on average, but the standard deviation is 1/2 lb. Assuming that the weight of the bags is normally distributed
To find : How you would find the weight range that 95% of the bags fall within?
Solution :
We have given,
Mean is
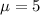
Standard deviation is
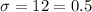
The critical value for a 95% confidence interval is 1.96.
Let x=1.96
The formula to find the range or confidence interval is
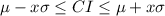
Substitute the value in the formula,

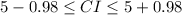
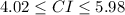
Therefore, The range that 95% of the bags fall within is (4.02,5.98)