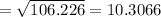Answer:
A. The mean age of the ten people at a party is: 34.2
B. The standard deviation is: 10.3066
Explanation:
We are given a information about the age of ten people as:
Age(in years) Number of people
30 5
32 3
31 1
65 1
Hence, the mean of the age is calculated as:
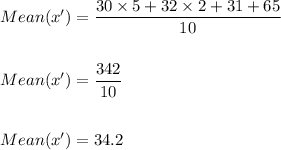
Now, we calculate the standard deviation in the following steps:
x x-x' (x-x')²
30 -4.2 17.64
30 -4.2 17.64
30 -4.2 17.64
30 -4.2 17.64
30 -4.2 17.64
32 -2.2 5.06
32 -2.2 5.06
32 -2.2 5.06
31 -3.2 10.24
65 30.8 948.64
∑ (x-x')²= 1062.26
Variance=∑ (x-x')²/10=106.226
Hence, standard deviation is the square root of variance.
standard deviation is: