On Monday, Moira doees 1/2 her homework. (1/2 remains)
On Tuesday, Moira does 1/2 of 1/2 = 1/4 of her homework. (1/4 remains)
On Wednesday, Moira does 1/2 of 1/4 = 1/8 of her homework. (1/8 remains)
On Thursday, Moira does 1/2 of 1/8 = 1/16 of her homework. (1/16 remains)
On Friday, she must do the remaining homework: 1/16 of the original amount.
Using exponents, the homework (hn) that Moira accomplishes on day n is
... hn = (1/2)^n
Since Moira does half each day, the amount left undone is equal to the amount done. The amount left undone on Thursday (for Friday) is equal to the amount done on Thursday:
... h4 = (1/2)^4 = 1/16
_____
Perhaps you're to sum the amounts done and subtract that from the total. That's going at it the long way around, but will get you the same result.
(Needed to be done on Friday) = 1 - ∑[n=1,4] (1/2)^n = 1 - (1/2)((1/2)^4-1)/(1/2 -1)
... = (1/2)^4 = 1/16
The sum of n terms of a geometric sequence is given by
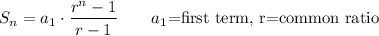
Here, we have
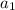 = 1/2 and r = 1/2. Then the sum of 4 terms is as shown above.
= 1/2 and r = 1/2. Then the sum of 4 terms is as shown above.