Question

URGENT!!!!!!!!!!! The height, h, in feet of a ball suspended from a spring as a function of time, t, in seconds can be modeled by the equation h=asin(b(t-h))+k. What is the height of the ball at its equilibrium?

A. a feet
B. b feet
C. h feet
D. k feet

Answer 1

Option D - Height of the ball at its equilibrium is given by k feet.

Step-by-step explanation:

Given : The height, h, in feet of a ball suspended from a spring as a function of time, t, in seconds can be modeled by the equation
`h=asin(b(t-h))+k`.

To find : What is the height of the ball at its equilibrium?

Solution :

The general form of sin function is
`y=Asin(Bx)+C`

Where A is the amplitude

B is the
`(2\pi )/(Period)`

C is the midline

Midline is the line that runs between the maximum and minimum y- values of the function.

Midline is given by y=C

Comparing the given function with the general form.

Midline C=k

i.e, h=k

Height of the ball at its equilibrium is given by k feet.

Therefore, Option D is correct.

Answer 2

The correct answer is: k feet (Option D)

Step-by-step explanation:

Let me solve it without using any complex jargon (and formulas).

Given equation is as follows:

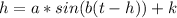`h = a*sin(b(t-h)) + k` ---- (A)

Here in this case, a represents the distance of the ball from the equilibrium position WHEN the spring is stretched. h inside the sine function represents the horizontal phase shift. Please do not confuse it with the height, and k represents the vertical shift.

Before oscillations, the amplitude is equal to zero. Assume that the ball attached with the spring was pushed down to position a and let go (as shown in the figure below). Now the ball would oscillate between the +a and -a. Why? Because the maximum value of sine function—sin(b(t-h)) (given in the above equation)—is +1, and the minimum value will be -1. When sin(b(t-h)) will be multiplied by a, the maximum value of a*sin(b(t-h)) will be +a, and the minimum will be -a. However, there is a vertical shift, k, involved in the equation as well. Now the maximum value of (a*sin(b(t-h)) + k) will be (+a+k), since the maximum value of a*sin(b(t-h)) is +a. Likewise, the minimum value of (a*sin(b(t-h)) + k) will be (-a+k), since the minimum value of a*sin(b(t-h)).

The equilibrium position lies between (+a+k) and (-a+k). To find the equilibrium position, add both of them and divide it by 2.

At equilibrium position, height, will be:

`((a+k) + (-a+k))/(2) = (0+2k)/(2) = k\thinspace feet`

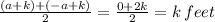
Hence, the height of the ball at its equilibrium is k feet (Option D).