If you expand the left hand side, the inequality becomes
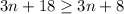
As you can see,
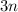appears on both sides, which means that it cancels out. You can subtract
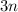from both sides to get
and this is clearly always true. If you interpreted the inequality with words, it would sound like
"For which values of n is 18 greater than 8"
Since the inequality does not depend on n anymore and the remaining part is true (18 is indeed greater than 8), every possible value of n satisfies the inequality.