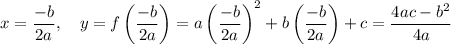Question

Find the smallest possible value of a quadratic equation

Answer 1

I'm assuming that you mean to find the minimum of a parabola, i.e. the minimum of a function defined as

`f(x) = ax^2+bx+c,\quad a,b,c \in\mathbb{R},\quad a\\eq 0`

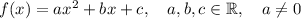
To find the minimum of a function, we have to find a point
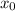`x_0` such that

`f'(x_0) = 0,\quad f''(x_0) > 0`

The first derivative is

`f'(x) = 2ax+b \implies f'(x)=0 \iff x = (-b)/(2a)`

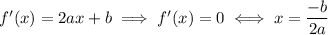
The second derivative is

`f''(x) = 2a`

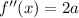
So, a parabola has a minimum only if
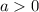`a>0` (otherwise, the parabola is concave down and it has no lower bound). In that case, the minimum has coordinates

`x = (-b)/(2a),\quad y = f\left((-b)/(2a)\right) = a\left((-b)/(2a)\right)^2 + b\left((-b)/(2a)\right) + c = (4ac-b^2)/(4a)`