Question

MATH- ALGEBRA 1- SHOW WORK PLEASE

What is the average rate of change of the function over the interval x = 0 to x = 8?

f(x)=2x+3/3x−3
Enter your answer, as a fraction

(answer is 5/21 but i need someone to show the work)

Answer 1

Rates are essentially the same as ratios - they're comparisons of two different values by division. Our goal in finding a rate is to find how the two values involved relate to each other, and in this problem, we want to find how much some change in x relates to some change in f(x). By convention, we make this comparison by dividing the change in f(x) by the change in x, frequently written as Δf(x) and Δx. Symbolically, this looks like

`(\Delta f(x))/(\Delta x)`

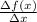
We measure the change in some value through subtraction - here, we're given the values x = 0 and x = 8, so we can subtract one from the other to say that Δx = 8 - 0 = 8.

To find Δf(x), we first need to find two appropriate values to compare. Since we're given x = 0 and x = 8, we'll choose f(0) and f(8). Here are the calculations for those:

`f(0)=(2(0)+3)/(3(0)-3) =(3)/(-3) =-1`

`f(8) = (2(8)+3)/(3(8)-3)=(16+3)/(24-3)=(19)/(21)`

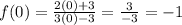
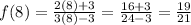
We can then find Δf(x) by finding f(8) - f(0):

`\Delta f(x)=(19)/(21)-(-1)=(19)/(21)+1=(19)/(21) +(21)/(21)=(40)/(21)`

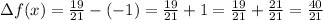
We can now return to our rate and substitute the values Δx = 8 and Δf(x) = 40/21 to get the ratio

`((40)/(21))/(8)`

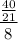
since fractions are another way of writing division, and since dividing by a number is the same as multiplying by its reciprocal, we can rewrite this ratio as

`((40)/(21))/(8) =(40)/(21)/8=(40)/(21)*(1)/(8)`

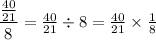
40 and 8 have the factor 8 in common, so we can cross cancel to reduce 40 to 5 and 8 to 1 (since 40 = 8 x 5 and 8 = 8 x 1), finally giving us

`(40)/(21)*(1)/(8)=(5)/(21)*(1)/(1)=(5)/(21)`

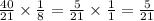
which is the answer we were looking for.

Answer 2

The average rate of change would be the change in y/the change in x. You must enter the x values into the function to get the corresponding y values. We’ll call x=0 x1, and we’ll call x=8 x2. y1 will be the y value corresponding to x1, and y2 will be the y value corresponding to x2. Finding the change in y would be y2–y1, and the change in x would be x2–x1.