Question

INFINITE SERIES

Determine if the series converges or diverges. For convergent series, find the sum of the series.
I know the answer, but I don’t know how to get to it.

Answer 1

The series is convergent and is equal to 1.

General Formulas and Concepts:

Algebra I

• Terms/Coefficients
• Factoring

Pre-Calculus

• Partial Fraction Decomposition

Calculus

Limits

• Limit Rule [Variable Direct Substitution]:
  `\displaystyle \lim_(x \to c) x = c`
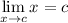
• Limit Property [Addition/Subtraction]:
  `\displaystyle \lim_(x \to c) [f(x) \pm g(x)] = \lim_(x \to c) f(x) \pm \lim_(x \to c) g(x)`

Sequences

Series

• Definition of a convergent/divergent series
• Sum of a series:
  `\displaystyle \lim_(n \to \infty) S_n`

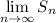
Telescoping Series:
`\displaystyle \sum^\infty_(k = 1) (b_1 - b_(k + 1)) = (b_1 - b_2) + (b_2 - b_3) + (b_3 - b_4) + ... + (b_1 - b_(k + 1)) + ...`

Explanation:

Step 1: Define

Identify

`\displaystyle \sum^\infty_(k = 1) (2k + 1)/(k^2(k + 1)^2)`

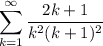
Step 2: Rewrite Sum

1. Factor:
   `\displaystyle \sum^\infty_(k = 1) (2k + 1)/(k^2(k + 1)^2) = \sum^\infty_(k = 1) (2k + 1)/(k \cdot k(k + 1)(k + 1))`
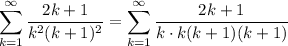
2. Break up [Partial Fraction Decomposition]:
   `\displaystyle (2k + 1)/(k^2(k + 1)^2) = (A)/(k) + (B)/(k^2) + (C)/(k + 1) + (D)/((k + 1)^2)`
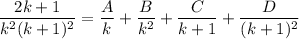
3. Simplify [Common Denominator]:
   `\displaystyle 2k + 1 = Ak(k + 1)^2 + B(k + 1)^2 + Ck^2(k + 1) + Dk^2`
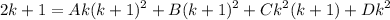
4. [Decomp] Expand:
   `\displaystyle 2k + 1 = Ak^3 + Ck^3 + A2k^2 + Bl^2 + Ck^2 + Dk^2 + Ak + B2k + B`
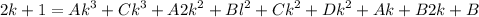
5. [Decomp] Factor:
   `\displaystyle 2k + 1 = k^3(A + C) + k^2(2A + B + C + D) + k(A + 2B) + B`
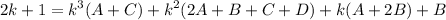
6. [Decomp] Set up systems:
   `\displaystyle \begin{cases} A + C = 0 \\ 2A + B + C + D = 0 \\ A + 2B = 2 \\ B = 1 \end{cases}`
7. [Decomp] Solve:
   `\displaystyle A = 0, \ B = 1, \ C = 0, \ D = -1`
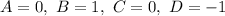
8. [Decomp] Substitute in variables:
   `\displaystyle (2k + 1)/(k^2(k + 1)^2) = (0)/(k) + (1)/(k^2) + (0)/(k + 1) + (-1)/((k + 1)^2)`
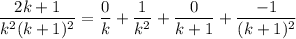
9. [Decomp] Simplify:
   `\displaystyle (2k + 1)/(k^2(k + 1)^2) = (1)/(k^2) - (1)/((k + 1)^2)`
10. Substitute in decomp [Sum]:
    `\displaystyle \sum^\infty_(k = 1) (2k + 1)/(k^2(k + 1)^2) = \sum^\infty_(k = 1) \bigg( (1)/(k^2) - (1)/((k + 1)^2) \bigg)`

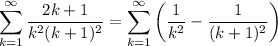
Step 3: Find Sum

1. Find Sₙ terms:
   `\displaystyle \sum^\infty_(k = 1) \bigg( (1)/(k^2) - (1)/((k + 1)^2) \bigg) = \bigg( 1 - (1)/(4) \bigg) + \bigg( (1)/(4) - (1)/(9) \bigg) + \bigg( (1)/(9) - (1)/(16) \bigg) + ... + \bigg( (1)/(k^2) - (1)/((k + 1)^2) \bigg) + ...`
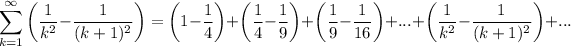
2. Find general Sₙ formula:
   `\displaystyle S_n = 1 - (1)/((k + 1)^2)`
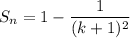
3. Sum of a series:
   `\displaystyle \sum^\infty_(k = 1) (2k + 1)/(k^2(k + 1)^2) = \lim_(n \to \infty) \bigg( 1 - (1)/((k + 1)^2) \bigg)`
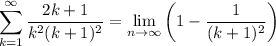
4. Evaluate limit [Limit Rule - Variable Direct Substitution]:
   `\displaystyle \sum^\infty_(k = 1) (2k + 1)/(k^2(k + 1)^2) = 1 - 0`
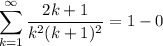
5. Simplify:
   `\displaystyle \sum^\infty_(k = 1) (2k + 1)/(k^2(k + 1)^2) = 1`

∴ the sum converges to 1 by the Telescoping Series.

Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Convergence Tests (BC Only)

Book: College Calculus 10e