Question

If A ⊂ B, then which of the following describes the relationship between A and B?

1. Set A can have the same number of elements as set B.
2. Set B may have less elements than set A.
3. The intersection of sets A and B must be the empty set.
4. Set B may have more elements than A does.

Answer 1

The answer is 4 alone, or 1 and 4, depending on how you interpret the symbol (see below for explanation).

The writing
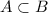`A \subset B` means that A is a subset of B. This means that every element of A is also an element of B, while there are elements of B that are not elments of A. For example, even numbers are a subset of natural numbers: all even numbers are natural numbers, but not all natural numbers are even.

In theory, a subset could "fill" the whole superset (and thus they are the same set), but this is indicated by the writing
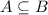`A \subseteq B`. Nevetheless, sometimes the two symbols are interchanged, and one writes
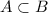`A \subset B` but means
`A \subseteq B`.

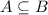You can think of this as the same difference between
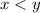`x<y` and
`x \leq y`

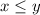
So, the first point is false if you mean that A is a "strict" subset of B, while it can be true if you mean that A is generally a subset of B.

As for the second point, set B can't have less elements than set A. In this case, there would be an element in A not belonging to B, which is impossibile because B is a superset of A.

Third point: the intersection can't be the empty set (unless A is empty), because every element in A also belongs to be, and so the intersection between A and B is actually A itself.

Finally, the fourth point is true: basing on everything we said so far, B contains at least all the elements in A, and possibly some more.