Question

Simplify cube root of 7 over fifth root of 7.

7 to the power of 1 over 5
7 to the power of 8 over 15
7 to the power of 5 over 3
7 to the power of 2 over 15

Answer 1

So to put your equation into algebraic terms, your asking for
`\frac{\sqrt[3]{7}}{\sqrt[5]{7}}` .

Firstly, we have to convert these into fractional exponents. The rule to do that is
`x^{(m)/(n)}=\sqrt[n]{x^m}` . Applying that here, our equation is
`\frac{7^{(1)/(3)}}{7^{(1)/(5)}}`

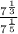
Next, the rule with dividing exponents with the same base is to just subtract the exponents, so with this we are subtracting 1/5 from 1/3. However, we need to find their LCM, or lowest common multiple, of 3 and 5. You can do this by listing out what numbers 3 and 5 are factors of. In this case, the LCM is 15. Multiply 1/3 by 5/5 and 1/5 by 3/3:

`(1)/(3)*(5)/(5)=(5)/(15)\\ \\ (1)/(5)*(3)/(3)=(3)/(15)\\ \\ \frac{7^{(5)/(15)}}{7^{(3)/(15)}}`

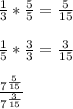
Now that they share the same denominator, subtract the numerators of the 2 fractional exponents and your answer will be
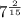`7^(2)/(15)`, or the last option.