By definition, we have

So, we have to solve two different equations, depending of the possible range for the variable. We have to remember about these ranges when we decide to accept or discard the solutions:
Suppose that
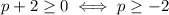
In this case, the absolute value doesn't do anything: the equation is
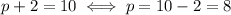
We are supposing
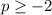 , so we can accept this solution.
, so we can accept this solution.
Now, suppose that
 . Now the sign of the expression is flipped by the absolute value, and the equation becomes
. Now the sign of the expression is flipped by the absolute value, and the equation becomes
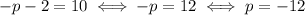
Again, the solution is coherent with the assumption, so we can accept this value as well.