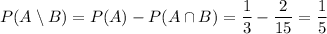Question

IF P(A)=1/3, P(B)=2/5, and P(AuB)=3/5, what is P(A^B)?

Answer 1

The probability of the union of two events is the sum of their probability, minus the probability of their interserction:

`P(A \cup B) = P(A) + P(B) - P(A \cap B)`

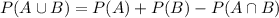
If we plug the known values into this formula, we have

`(3)/(5) = (1)/(3) + (2)/(5) - P(A\cap B)`

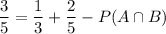
From which we can deduce

`P(A\cap B) = (1)/(3) + (2)/(5) - (3)/(5) = (2)/(15)`

So, the probability of
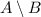`A \setminus B` is a bit less than
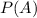`P(A)`, we have to take away all events that belong to B as well:

`P(A \setminus B) = P(A) - P(A\cap B) = (1)/(3) - (2)/(15) = (1)/(5)`