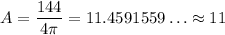Question

A circle measure 12 feet in diameter what’s its area to the nearest foot

Answer 1

The formulas for the circumference and area of a circle are

`C = 2\pi r,\quad A = \pi r^2`

So, if we isolate the radius from the formula for the circumference we have

`r = (C)/(2\pi)`

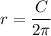
And if we substitute this expression for the radius in the formula for the area, we have

`A = \pi r^2 = \pi (C^2)/(4\pi^2) = (C^2)/(4\pi)`

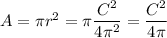
So, if you plug your value you have

`A = (144)/(4\pi) = 11.4591559\ldots \approx 11`