Answer: The standard deviation of the sampling distribution of the average (sample mean) score for the 36 students= 1
Explanation:
The standard deviation of the sampling distribution of mean is given by :-
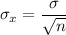
, where
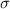 = population standard deviation.
= population standard deviation.
n= sample size.
Given : The scores of individual students on the american college testing (act) program composite college entrance examination have a normal distribution with mean 18.6 and standard deviation 6.0. at north-side high.
i.e.
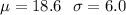
Sample size : n= 36
Then, the standard deviation of the sampling distribution of the average (sample mean) score for the 36 students will be :-
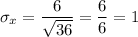
Hence, The standard deviation of the sampling distribution of the average (sample mean) score for the 36 students= 1