It is given in the question that,
At most, Keith can spend $90 on sandwiches and chips for a company lunch. He already bought chips for $15 and will buy sandwiches that cost $6 each. The inequality
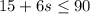
represents the described cost, where s is the maximum number of sandwiches that could be bought.
Now we have to solve for s, and for that, we first subtract 15 to both sides, that is
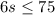
Dividing both sides by 6

So the maximum number of sandwiches Keith can buy is 12.