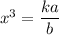Remark.
The easiest way to do this is simply to leave the givens alone and divide. Parts of it will cancel out. You can't always do this, but this question is an example of leaving things be.
Step One
Divide the two expressions
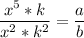
Now you use the index laws to get what you need. Forget the ks on the left for a second and just work with the xs.
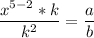
The law of indices says that it you want to bring the power of the same base to the numerator, you write the base in the numerator, and subtract the power that was in the denominator from the power in the numerator. x^(5 - 2) in this case.
Step Two
Next deal with the ks.
The same law applies for the ks. You subtract the power shown in the numerator from the power of the k in the denominator, in this case 1/k^(2 - 1)
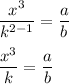
Step Three
The last step is to multiply both sides by k
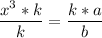
Giving as your final answer