Step 1: Assign variable for the unknown that we need to find.
Let 'p' be the price/pound in dollars, 's' be the supply in millions of pounds, and 'd' be the demand in millions of pounds.
Step 2: List the information from the given statement.
Statement : Assume that at a price of $2.00 per pound, the annual supply of coffee beans in Country A is 8 million pounds, while the demand is 10 million pounds. At a price of $3.00 per pound, the supply is 10.2 million pounds, and the demand is 8.6 million pounds.
From the above statement we can list the two points for supply and demand function as below:

Step 3: Use the Slope formula and Point-Slope form of an equation to write equation representing the price-supply function & price-demand function.

Slope of Price-Supply function:

Equation of Price-Supply function:

Slope of Price-Demand function:
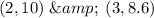

Equation of Price-Demand function:

Step 4: Finding the equilibrium point
Equilibrium point is the point were the supply and demand function will be equal to each other.

Substituting the p value in any one of the function we get...
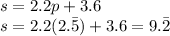
Conclusion:
The attached graph shows the equilibrium point, supply and demand function.