Question

If an object is dropped from a height of 144 feet, the function h(t) = -16t2 + 144 gives the height of the object after t seconds. When will the object hit the ground?

A) 9 seconds

B) 6 seconds

C) 1.5 seconds

D) 3 seconds

Answer 1

So this question is asking for the zeros, or the x-intercepts, of this equation. For this, we have to set h(t) to zero to solve for it.

For this, we will be using the quadratic formula, which is
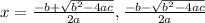`x=(-b+√(b^2-4ac))/(2a),(-b-√(b^2-4ac))/(2a)` (a = t^2 coefficient, b = t coefficient, and c = constant). In this case, our equation is
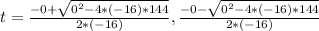`t=(-0+√(0^2-4*(-16)*144))/(2*(-16)),(-0-√(0^2-4*(-16)*144))/(2*(-16))` . From here we can solve for t.

1. Firstly, solve the exponents and multiplications:
   `t=(-0+√(0+9216))/(-32),(-0-√(0+9216))/(-32)`
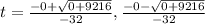
2. Next, solve the additions and subtractions:
   `t=(√(9216))/(-32),(-√(9216))/(-32)`
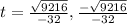
3. Next, square root 9216:
   `t=(96)/(-32),(-96)/(-32)`
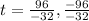
4. Lastly, divide and your answers are going to be
   `t=-3,3`

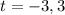
Since we cannot have negative time, the object hits the ground at 3 seconds, or D.