Question

Suppose that the ages of cars driven by employees at a company are normally distributed with a mean of 8 years and a standard deviation of 3.2 years.

What is the z-score of a car that is 9.1 years old?

Answer 1

There follows the formula for "z-score:"

raw score - mean

z = ------------------------------

standard dev

9.1 - 8

Here, the z-score is z = ------------- = 0.344

3.2

Answer 2

Answer: The z-score of a car is 0.34375.

Explanation:

Since we have given that

The ages of cars driven by employees at a company are normally distributed.

Mean =
`\mu` = 8 years

Standard deviation =
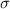`\sigma` = 3.2 years

Age of car = X = 9.1 years old.

We need to find the z-score of a car which is given by

`z=\frac{X-\mu}\sigma}\\\\z=(9.1-8)/(3.2)\\\\z=(1.1)/(3.2)\\\\z=0.34375`

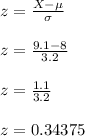
Hence, the z-score of a car is 0.34375.